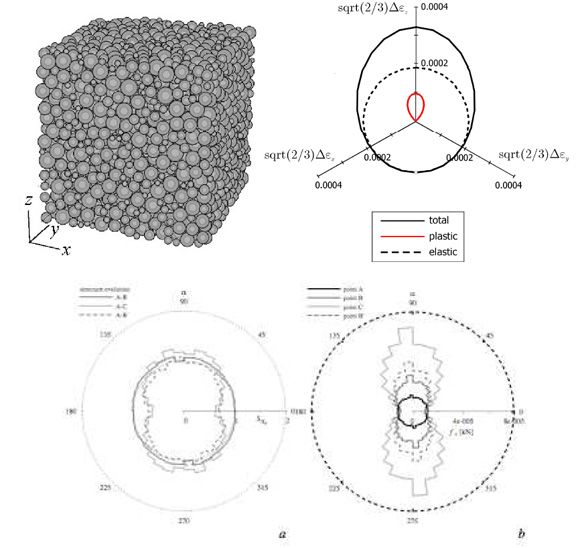
a) Applicazione del metodo degli elementi distinti (DEM) allo studio della nonlinearità incrementale dei mezzi granulari.
Il metodo degli elementi distinti (DEM) è utilizzato per investigare a livello macroscopico il comportamento meccanico dei mezzi granulari, mediante la simulazione di percorsi di carico controllati su un volume elementare rappresentativo (REV). Tale strategia è utilizzata anche per la messa a punto di metodi multiscala FEM-DEM, nei quali la descrizione della risposta del materiale è fornita dal modello numerico alla microscala anziché da una equazione costitutiva fenomenologica.
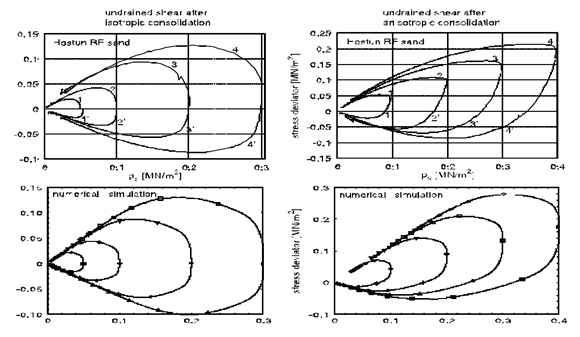
b) Modellazione costitutiva del comportamento meccanico di mezzi granulari (a grana fine ed a grana grossa) nell’ambito della teoria della plasticità.
La teoria della plasticità incrudente, con incrudimento isotropo e anisotropo, è utilizzata per lo sviluppo di modelli costitutivi capaci di descrivere il comportamento non lineare, inelastico, ed “history-dependent” dei terreni a grana fine ed a grana grossa, in condizioni di carico monotoniche o cicliche. Per l’applicazione dei modelli costitutivi sviluppati in questo ambito alla soluzione di problemi al finito, particolare attenzione è rivolta alla messa a punto di strategie algoritmiche per l’integrazione numerica (a livello locale) delle leggi di evoluzione delle variabili di stato, mediante algoritmi impliciti (Generalized Return Mapping Algorithms) ed espliciti (algoritmi di Runge-Kutta “embedded”, con time-stepping adattativo e controllo dell’errore).
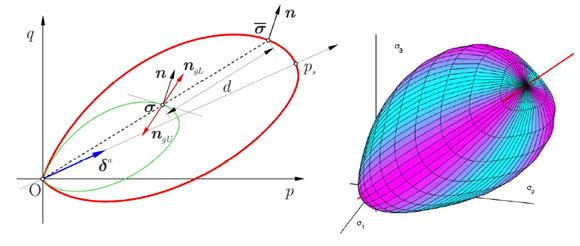
c) Modellazione costitutiva del comportamento meccanico di mezzi granulari (a grana fine ed a grana grossa) nell’ambito della teoria dell’ipoplasticità.
Una possibile alternativa alla descrizione del comportamento inelastico ed “history-dependent” dei terreni a grana fine ed a grana grossa è rappresentato dalla teoria dell’Ipoplasticità, caratterizzata dall’assenza di decomposizione delle velocità di deformazione in componenti reversibile ed irreversibile, e dalla dipendenza continua della risposta del materiale dalla direzione del percorso di sollecitazione imposto (nonlinearità incrementale). Tale caratteristica risulta particolarmente importante nella previsione delle condizioni di innesco dei processi di rottura con localizzazione delle deformazioni in bande di taglio. Per l’applicazione dei modelli costitutivi sviluppati in questo ambito alla soluzione di problemi al finito, particolare attenzione è rivolta alla messa a punto di strategie algoritmiche per l’integrazione numerica (a livello locale) delle leggi di evoluzione delle variabili di stato, mediante algoritmi impliciti (Generalized Return Mapping Algorithms) ed espliciti (algoritmi di Runge-Kutta “embedded”, con time-stepping adattativo e controllo dell’errore).